CONJUNTOS NUMÉRICOS. DIVISIBILIDAD
-¿Cuántos conjuntos numéricos conoces?¿Sabes representarlos?
-¿Controlas sus operaciones y propiedades?
¿Qué vamos a trabajar?
1.- Clasificación de los números reales.2.-Reglas de divisibilidad
3.-Descomposición Factorial
4.-Máximo común divisor
5.-Mínimo común múltiplo
El conjunto de los números reales está formando por:
1.- Copia los siguientes problemas e intenta resolverlo:
"PROBLEMA 1: Pilar está organizando una coreografía formada por 48 bailarines. Para organizarlos, tiene que colocarlos de forma que en todas las columnas haya el mismo número de bailarines. ¿De cuantas formas posibles puede colocarlos?"
-Recuerda: calcular los divisores de un número: Para calcular los divisores de un número vamos dividiendo por todos los números menores que el en orden ascendente y viendo si el resto es 0. Obtendremos todos los números posibles cuando el cociente sea menor que el divisor.
48 = 1·48 = 2·24 = 3·16 = 4·12 = 6·8
48:5 no es exacto.
48:7 no es exacto.
Div(48)={1, 2, 3, 4, 6, 8, 12, 16, 24 , 48}
"PROBLEMA 2: Juan tiene 30 caramelos y los quiere repartir de forma equitativa entre sus 9 amigos y él. ¿Cuántos caramelos tendrá que repartir a cada uno?
Si de los 30 caramelos a cada amigo le corresponden 2. ¿Cuántos amigos son en total?"
¿Cómo lo has calculado?
Un número es divisor/factor de otro si se puede dividir de forma exacta el segundo por el primero.
2.-Copia el siguiente problema e intenta resolverlo:
"PROBLEMA 3: Un semáforo se pone en rojo cada 2 minutos y otro cada 3. Si a las tres de la tarde se ponen rojos al mismo tiempo, ¿A qué hora volverán a ponerse rojos los dos a la vez? ¿Cuántas veces se pondrán rojos a la vez en una hora?"
Un número es múltiplo de otro si es el resultado de multiplicar el segundo por algún número natural.
Ejemplos: 18; 36; 2
Como 36:18=2 división exacta tenemos que:
36 es ________________ de ______________
18 y 2 son ____________________ de ___________
TRUCO: Si dos números son multiplos de otro, su suma también lo es.
Ejemplo: 28 y 77 son múltiplos de 7 --> 28+77=105 es múltiplo de 7.
Para que sea más fácil es importante memorizar los criterios de divisibilidad. Además, nos servirán para calcular el MCD y el mcm.
-Reglas de divisibilidad:
-Números primos y compuestos:
Un número es primo si sólo tiene dos divisores, el 1 y él mismo.
Un número es compuesto si tiene más de dos divisores.
EL 1 NO ES PRIMO Y COMPUESTO, sólo tiene un divisor, él mismo.
Recuerda: Determinar si un número es primo o no. Pasos:
1º Usar los criterios de divisibilidad.
2º Ir dividiendo hasta encontrar un resto cero, o un cociente menor que el divisor.
Ejemplos:
29
No es divisible por 2, por 3, ni por 5. (5·5=25)
Tampoco es divisible por 6, ya que no es múltiplo ni de 2 ni de 3.
COMO 6·6=36>29. No hace falta seguir.
247
no es divisible por 2, 3, 5, 7, 11, 13, 17
24-7·2=10; 247:17=14 y resto 9. Como 14<17 tenemos que 247 es primo.
Criba de Eratóstenes
La criba de Eratóstenes es un algoritmo que permite hallar todos los números primosmenores que un número natural dado.
Ejercicio: Busca en internet la criba de Eratóstenes y aplícala para calcular los números primos entre 1 y 200.
DESCOMPOSICIÓN FACTORIAL
Para descomponer un número en factores primos, se siguen 3 pasos:
1º Se busca un divisor primo del número. (Empezamos en orden de menor a mayor)
2º Se divide el número entre el divisor primo encontrado.
3º Se repite el proceso hasta que el cociente que obtengamos sea 1.
4º Expresamos el número
PROBLEMA 4: "Han llegado 30 cajas al almacén. ¿De cuántas maneras distintas se pueden apilar de forma que en todos los montones haya el mismo número de cajas?
-Nos piden las formas posibles, para ello usaremos la siguiente propiedad:
PROPIEDAD:
Para saber cuántos divisores tiene un número, debemos sumar +1 a cada uno de los exponentes de sus factores primos y multiplicarlos. Por ejemplo:
18= 2 · 3; se calcula como (1+1) · (2 + 1) = 2 · 3 =6
Div 18={1 , 2, 3, 6, 9 , 18}
Ejercicio: Calcula el número de divisores de 48: (1º desc. Fact; 2ºAplico propiedad)
MÁXIMO COMÚN DIVISOR
El mcd de varios números es el mayor divisor común de los mismos.
Si queremos calcular el máximo común divisor de varios números lo que tenemos que hacer en primer lugar es descomponerlos en factores primos.
Ejemplo:
Tenemos que calcular el m.c.d.(40, 16)
1-Descomponemos en factores primos:
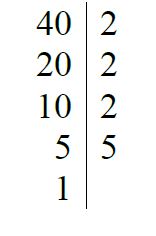

quedando:
40 = 23 . 5
16 = 24
De esta forma, elegimos el producto de los factores comunes elevados al menor exponente.
Por tanto:
El m. c. d. (40, 16) = 23 = 2. 2. 2. = 8
MÍNIMO COMÚN MÚLTIPLO
El m.c.m de varios números es el menor múltiplo común de dichos números.
Para calcularlo, elegimos el producto de los factores comunes y no comunes elevados al mayor exponente.
https://aula05mate.com/aritmetica/multiplos-y-divisores/





Comentarios
Publicar un comentario